
Félix Klein empieza su capítulo dedicado al Teorema de Taylor "trayendo al primer plano las series finitas, tan importantes el la práctica, y ayudando a la visión intuitiva de la situación con gráficos. De esta manera pareceran elementales y fácilmente comprensibles."
Estas aproximaciones pueden hacerse usando polinomios de grados cada vez mayores. Son fáciles de calcular y se aproximan a la curva en funciones que llamamos parábolas de osculación (parábolas osculatrices). Son los Polinomios de Taylor que obtenemos considerando los primeros términos de la Serie de Taylor de la función.
Se trata de investigar cómo y en qué intervalo estos polinomios representan curvas de aproximación útiles de las funciones.
En el caso de la función exponencial, conforme el grado del polinomio aumenta, las parábolas se aproximan a la función en un intervalo cada vez mayor.
El desarrollo de Taylor de la función exponencial en torno al 0 se expresa:
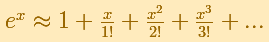
REFERENCIAS
ENLACES

|
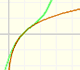
Polinomios de Taylor: función exponencial compleja
La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.
|

|
Función exponencial compleja
La función exponencial compleja extiende la función exponencial real al plano complejo.
|
|
Mercator y Euler: La función logaritmo
Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.
|
|
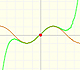
Polinomios de Taylor: función seno
Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.
|
|
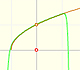
Polinomios de Taylor: raíz cuadrada
La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
|

|
Polinomios de Taylor: función racional 1
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
|
|
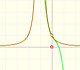
Polinomios de Taylor: función racional 2
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
|