Ángulo central e inscrito en una circunferencia: Caso III
El caso general del Teorema del ángulo central puede probarse usando el caso previo.
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
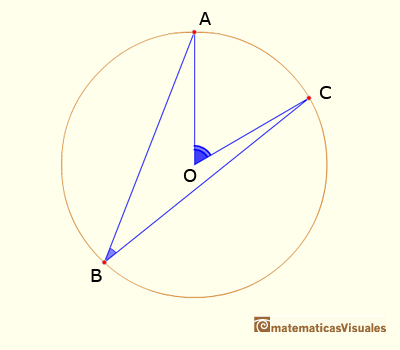
Para hacer esto, dibujamos un diámetro que pase por el vértice del ángulo inscrito. Entonces, dependiendo de la posición de los puntos, es suficiente sumar o restar dos ángulos.
En esta posición tenemos que sumar dos ángulos centrales (y usar el Caso II).
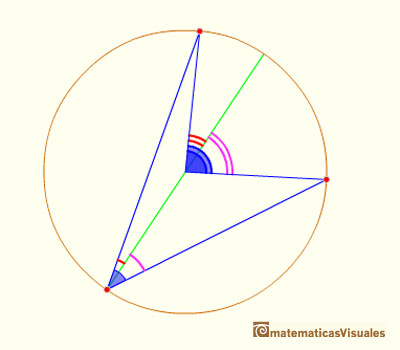
En esta posición tenemos que restar dos ángulos centrales (y usar el Caso II).
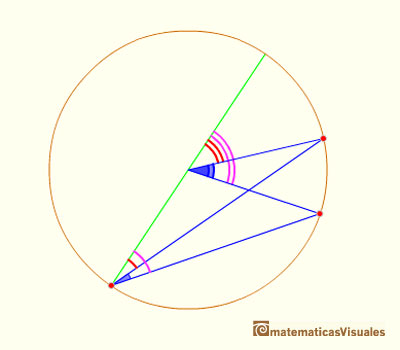
Con el Caso I, Caso II y este caso general hemos terminado la demostración del Teorema del ángulo central.
REFERENCIAS
Los Elementos de Euclides
SIGUIENTE
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.
ANTERIOR
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.
MÁS ENLACES
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.
Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.
A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.
Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.
La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.