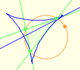
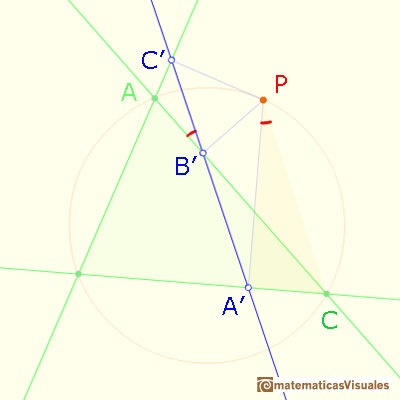
Partimos de un triángulo y su circunferencia circunscrita. Consideramos un punto
P en la circunferencia circunscrita del triángulo.
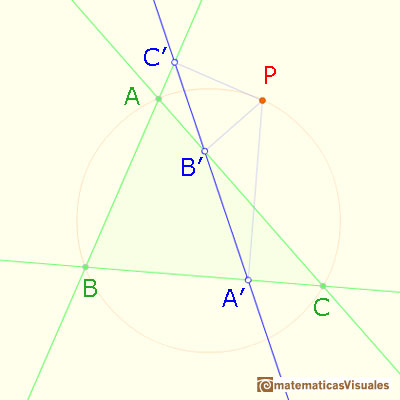
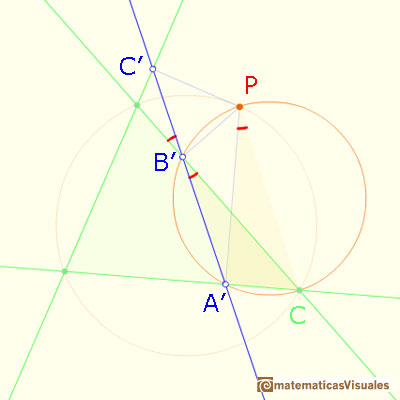
Los pies de las perpendiculares desde P
a los tres lados del triángulo están alineados (recta de Simson o de Simson-Wallace)
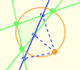
A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.
Vamos a demostrar esta propiedad usando esta notación:
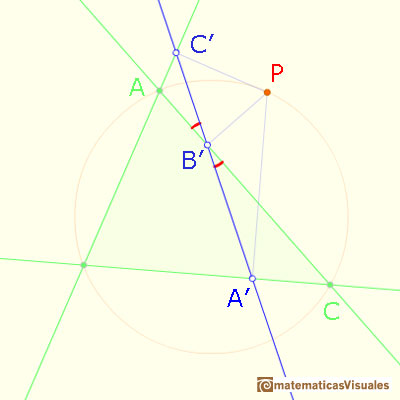
Hemos tomado el punto P en el arco AC que no contiene a B. Otros casos se obtienen renombrando A, B, C.
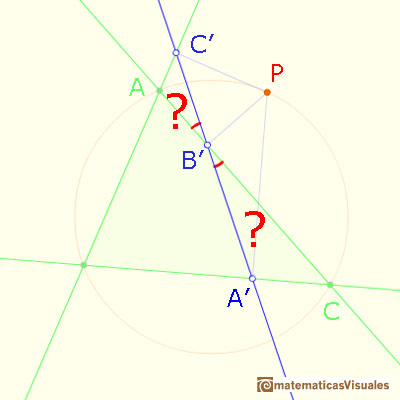
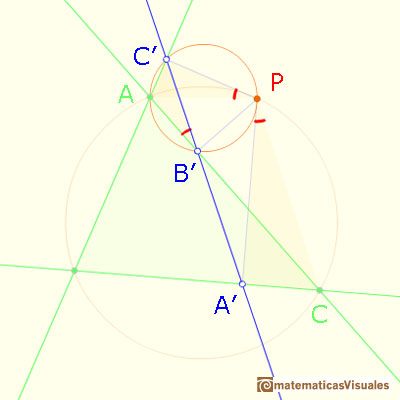
Si podemos probar que estos dos ángulos son iguales entonces los puntos A', B', C' serán colineales.
Usaremos una consecuencia de la propiedad de la circunferencia (Euclides, III.21 o III.22) que
dice que la suma de los ángulos opuestos de un cuadrilátero convexo inscrito en una circunferencia es igual a dos ángulos rectos.
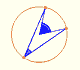
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
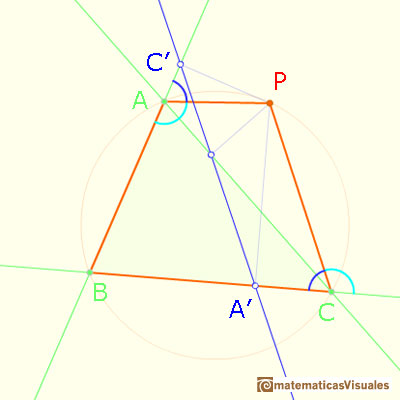
Estos dos triángulos rectángulos son semejantes, por lo tanto:
Los puntos A, B', P, C' están en una circunferencia:
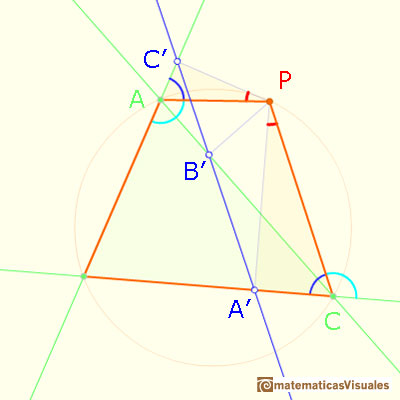
Y los puntos B',A',C,P también están en una circunferencia:
Por lo tanto, los puntos A', B', C' son colineales. La recta que forman se llama recta de Simson o recta de Simson-Wallace de P.
REFERENCIAS
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
MÁS ENLACES
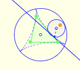
La construcción de la deltoide de Steiner como hipocicloide está relacionada con la circunferencia de los nueve puntos.
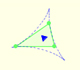
El triángulo equilátero determinado por la deltoide de Steiner tiene los lados paralelos al triángulo de Morley pero con orientación opuesta.

Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
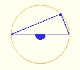
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.
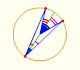
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.
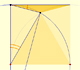
Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.
Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero (Triángulo de Morley).
Demostración muy bonita y visual de Conway. Podemos jugar con una animación interactiva y ver los diferentes pasos de la demostración.


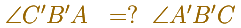
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR