El Deltoide de Steiner y las Rectas de Simson
Steiner demostró que la envolvente de las rectas de Wallace-Simson es una curva que tiene tres cúspides que se llama el Deltoide de Steiner.
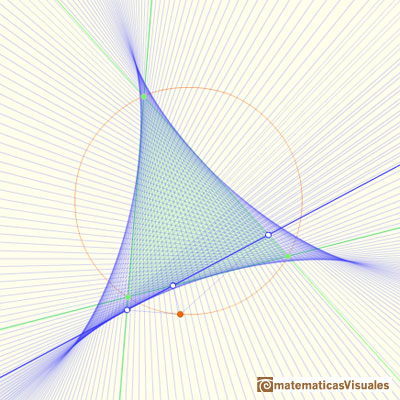
El Deltoide de Steiner es tangente a los tres lados del triángulo.
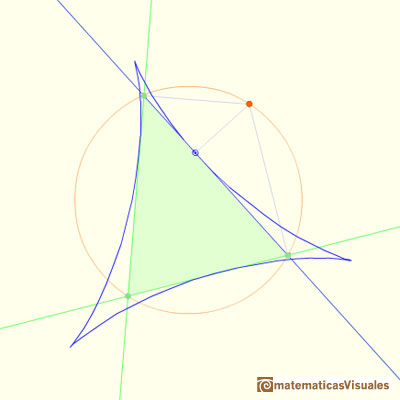
En este caso, ¿qué relación tiene el punto de la circunferencia circunscrita con algún vértice del triángulo?
El Deltoide de Steiner es tangente a las tres alturas del triángulo.
REFERENCIAS
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
de Guzmán, Miguel 'The envelope of the Wallace-Simson lines of a triangle. A simple proof of the Steiner theorem on the deltoid'.
RACSAM, vol. 95, 2001.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
SIGUIENTE
La construcción de la deltoide de Steiner como hipocicloide está relacionada con la circunferencia de los nueve puntos.
ANTERIOR
Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.
MÁS ENLACES
A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.
El triángulo equilátero determinado por la deltoide de Steiner tiene los lados paralelos al triángulo de Morley pero con orientación opuesta.
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.
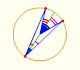
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.
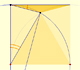
Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.
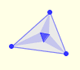
Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero (Triángulo de Morley).
Demostración muy bonita y visual de Conway. Podemos jugar con una animación interactiva y ver los diferentes pasos de la demostración.