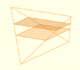
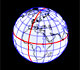
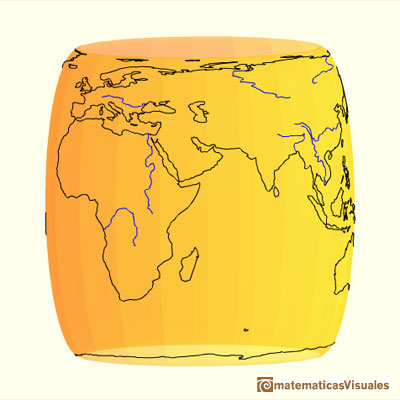
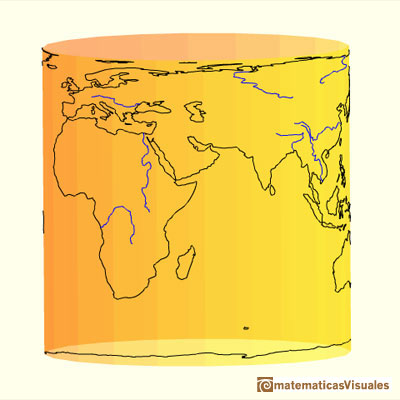
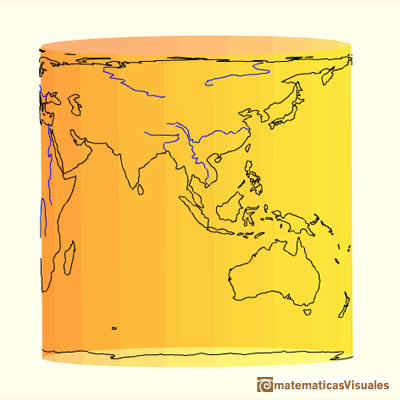
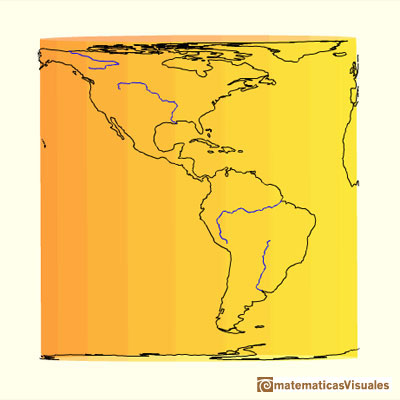
Vamos a estudiar una proyección de la esfera sobre un cilindro circunscrito. Cada punto de la esfera se proyecta horizontalmente sobre un cilindro tangente a la esfera. Es una proyección que preserva el área y que se ha utilizado para realizar mapas. El primero que la definió rigurosamente fue Johann H. Lambert (1772) aunque se entiende que ya era conocida por Arquímedes.
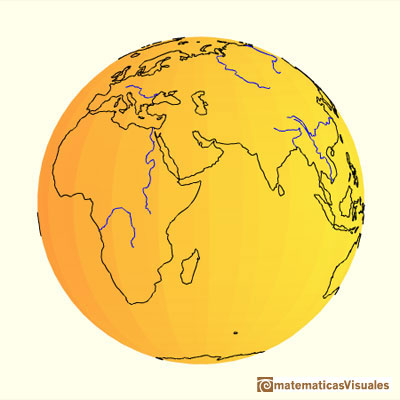
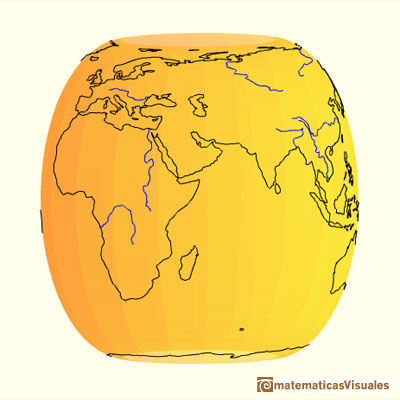
Hugo Steinhaus escribió sobre esta proyección:
"Si colocamos una esfera en un cilindro de modo que el cilindro sea tangente en el ecuador, y si proyectamos la esfera sobre la superficie cilíndrica prologando los planos de cada paralelo hasta cortar al cilindro y hacemos lo mismo con todos los planos de los meridianos, obtenemos en el cilindro un mapa de la esfera. Cortando el cilindro y desplegándolo plano obtenemos un mapa de la esfera con una red rectangular de meridianos y paralelos. Este mapa tiene la particularidad (ya conocida por Archímedes) de que conserva las áreas. Si entonces nos imaginamos la esfera cubierta por una capa de pintura o arcilla y llevamos cada partícula sobre su lugar apropiado en el cilindro, obtenemos un cilindro que está cubierto uniformemente por materia. Si la transferimos de vuelta hacia el eje común del cilindro y la esfera, cubriremos el eje uniformemente con materia."
En su libro 'Sobre la esfera y el cilindro', Arquímedes demostró la fórmula del área de la esfera.
El área de la esfera es igual al área lateral del cilindro tangente y es cuatro veces el área de un círculo máximo de la esfera.



A partir de este resultado podemos usar un argumento intuitivo y deducir el volumen de la esfera.
Seguimos a C.H.Edwards, que escribió en su libro 'The Historical Development of the Calculus':
"La relación entre V y el área S se basa en un argumento heurístio semejante al que podemos usar para relacionar el área de un círculo y la longitud de una circunferencia.

Podemos ver la esfera, aproximadamente, como una unión de una infinidad de pirámides que tienen el centro de la esfera como su vértice común y con sus bases formando una superficie poliédrica con una infinidad de caras inscritas en la esfera, cada una de las cuales casi coincide con una pequeña parte de la esfera.



Puesto que la altura de cada una de estas pirámides se hará prácticamente igual al radio de la esfera, y el volumen de una pirámide es un tercio del área de la base por la altura, parece evidente que
Entonces podemos derivar V a partir de S.
Arquímedes, en su libro 'Sobre la esfera y el cilindro' primero deduce el área de la esfera y después su volumen, pero en su libro 'El método' siguió la dirección opuesta y obtuvo S a partir de V.
Arquímedes escribió en su libro 'El método':
"A partir del teorema de que la esfera es cuatro veces el volumen del cono que tiene como base un círculo máximo de la esfera y su altura es igual al radio concebí la idea de la la superficie de la esfera es cuatro veces el área de un círculo máximo: pues, razonando a partir del hecho de que cualquier círculo es igual a un triángulo cuya base es igual a la circunferencia y su altura es igual al radio del círculo, comprendí que de un modo análogo, el volumen de cualquier esfera es igual al de un cono que tiene su base igual a la superficie de la esfera y su altura es igual a su radio" (citado por Edwards)
A pesar de que en tiempos de Kepler el libro de Arquímedes 'El método' estaba perdido, Kepler siguió un argumento similar para deducir la superficie de una esfera a partir de su volumen.

Kepler escribió un libro en 1615 sobre áreas y volúmenes de superficies y sólidos: Nova stereometria doliorum vinariorum (Nueva Geometría sólida de los barriles de vino). En este libro, Kepler pensó en una esfera como compuesta por una infinidad de pirámides o conos infinitesimales cada uno de ellos con su vértice en el centro de la esfera y cuyas bases formaban la superficie esférica.
Este es un ejemplo de un teorema sobre la esfera en el libro original de Kepler 'Nova stereometria doliorum vinariorum'. Podemos leer esta página, y el libro entero, en The Posner Memorial Collection,Carnegie Mellon University Libraries.
Una traducción puede ser: El área de una esfera es cuatro veces el área de un círculo máximo en la esfera.
Si recordamos el volumen y la superficie de un cilindro circunscrito a una esfera de radio r:

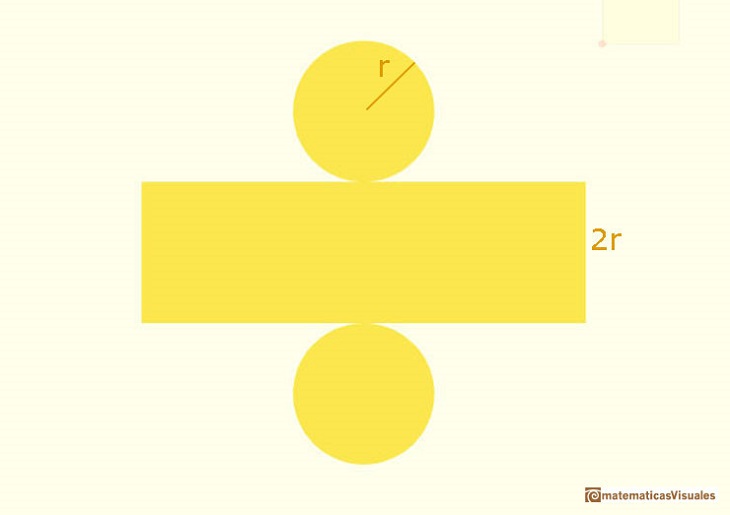
Entonces podemos comparar el área de una esfera y del cilindro:
Y también el volumen de la esfera y del cilindro:
Entonces podemos concluir que:
La razón entre la áreas de una esfera y del cilindro es la misma que la razón entre sus volúmenes.
Arquímedes estaba muy orgulloso de estos resultados y pidió que en su tumba se grabara una esfera inscrita en un cilindro circular recto que tuviera una altura igual a su diámetro.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES