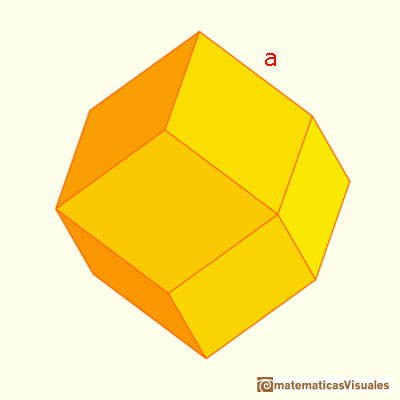
Ya hemos visto que el dodecaedro rómbico está relacionado con los panales de las abejas:

Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?
Y que podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo:

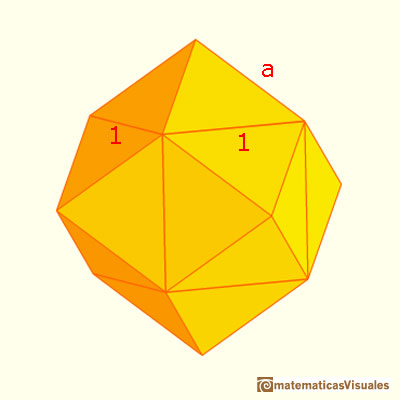
Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.
Cundy y Rollet escribieron sobre el dodecaedro rómbico y el cubo: "Si un cubo es dividido por seis planos diametrales que pasen por pares
de lados opuestos, se descompone en seis pirámides de base cuadrada. Si estas pirámides se añaden a las caras de otro cubo por fuera, el
resultado es un dodecaedro rómbico" (Cundy y Rollet, pág. 122)
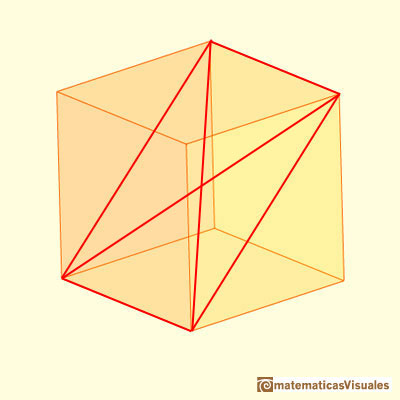
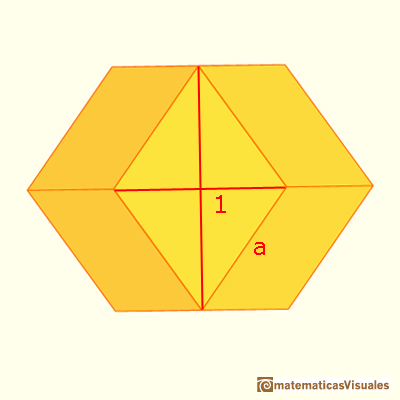
Un cubo se puede descomponer en seis pirámides congruentes de base cuadrada. Cuatro aristas de una pirámide son la mitad de la diagonal en el espacio del cubo.
Esta construcción tiene varias consecuencias interesantes.
Primero, podemos ver en la aplicación interactiva que estas seis pirámides llenan un cubo. El volumen de una de estas pirámides es un sexto del volumen del cubo.
Es decir, no necesitamos la fórmula del volumen de una pirámide para calcular el volumen de esta pirámide en particular.
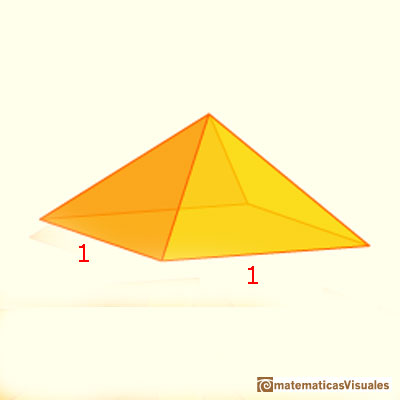
El volumen de una pirámide en general es un tercio del área de la base por la altura. Podemos comprobar que estas pirámides particulares verifican la fórmula:
el área de la base es 1 y la altura es 1/2.
Estas pirámides son un caso particularmente simple e importante de pirámide pues a partir de este ejemplo podemos deducir el volumen de pirámides de base
rectangular (expandiendo el cubo en tres direcciones).
La segunda consecuencia de esta construcción es que podemos calcular con mucha facilidad el volumen de un dodecaedro rómbico.
Recordamos que si dentro del dodecaedro rómbico hay un cubo de arista 1, entonces la longitud de la arista del dodecaedro rómbico es:
El volumen de este dodecaedro rómbico es el doble del volumen del cubo que hay en el interior:
Para calcular el volumen si la longitud de la arista es 1:
Entonces,
La fórmula general para calcular el volumen de un dodecaedro rómbico de arista a es:
Podemos jugar con la aplicación interactiva para ver simetrías muy bonitas como estas:
La tercera consecuencia de esta construcción es que el dodecaedro rómbico rellena o tesela el espacio.

Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.
Ya hemos visto que podemos construir una preciosa caja inspirada en las celdas de los panales de las abejas.

La Humanidad ha estdo siempre fascinada por cómo las abejas construyen sus panales. Kepler relacionó la forma de los panales con un poliedro que llamamos dodecaedro rómbico.
Ahora podemos construir un dodecaedro rómbico que tambien es una caja.
Se puede descargar el modelo, imprimirlo en cartulina y pegarlo. El diseñador de esta caja fue John Edminster y podemos encontrar referencias en
Beach Packaging Design.
El dodecaedro rómbico está relacionado con el cubo. Podemos construir un cubo y ponerlo dentro del dodecaedro rómbico. Dentro del cubo podríamos colocar un
cuboctaedro. En el caso que se muestra se trata de la Estrella Omega, una contrucción de origami fácil y bonita. Sólo se necesitan seis piezas de papel.
Si se imprimen los modelos con la misma impresora todo encaja: el dodecaedro rómbico, el cubo y el tamaño de los cuadrados de papel necesarios.
El dodecaedro rómbico también está relacionado con el octaedro. No nos extraña pues el cubo y el octaedro son poliedros duales.
También podemos construir un octaedro y ponerlo dentro del dodecaedro rómbico.
REFERENCIAS
Johannes Kepler - 'Strena seu De Nive Sexangula' ('Regalo de Año nuevo. Sobre el copo de nieve hexagonal', Traducción y notas de
Ana García Azcárate y Ángel Requena Fraile. Editorial Aviraneta, 2011. Este libro se puede descargar gratuitamente gracias a la generosidad
de sus autores a través del excelente sitio web de Ángel Requena 'Turismo Matemático' en su sección
Turismo Matemático. Libros descargables.
Johannes Kepler - 'De Nive Sexangula' (Tenemos una versión bilingüe en latin e inglés en
'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010.
Con notas y comentarios muy interesantes de Owen Gingerich y Guillermo Bleichmar. Las ilustraciones las realizó la matemática española Capi Corrales Rodrigáñez.
D'Arcy Thompson - On Growth And Form - Cambridge University Press, 1942. Traducción española de Ana María Rubio Díez y
Mario X. Ruiz-González publicada por Cambridge University Press.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. Una traducción española fue hecha por Luis Bou García y fue publicada por la Editorial
Salvat con el título 'Instantáneas Matemáticas' en 1986.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
W. Hope-Jones, 'The Rhombic Dodecahedron for the Young', The Mathematical Gazette, 1936.
Colin Maclaurin, 'On the Bases of the Cells wherein the Bees deposite their Honey', 1743.
D'Arcy Thompson, 'On Growth And Form' - Cambridge University Press, 1942.
L. Fejes Tóth, 'What the bees know and what they do not know', Bull. Amer. Math. Soc. 70 (1964). In
Project Euclid
D. Wallo, V. Duris, L. Rumanova, 'Geometry of bee cells rediscovered', The Electronic Journal of Mathematics and Technology.
Hermann Weil, 'Symmetry', pp. 83-92, Princeton University Press, 1952.
MÁS ENLACES

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.

Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.

Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.

Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.

Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.

El ángulo obtuso de las caras rómbicas del dodecaedro rómbico se conoce como ángulo de Maraldi. Solo se necesita un poco de trigonometría básica parar calcularlo.

Estudiando el empaquetamiento de esferas obtenemos el dodecaedro rómbico y el dodecaedro trapezo-rómbico. Su dual es el cuboctaedro girado.

A partir de un conocimiento básico del dodecaedro rómbico se puede calcular rápidamente la densidad del empaquetamiento óptimo de esferas.

Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
Traducción del artículo 'Kepler: The Volume of a Wine Barrel' publicado en 2012 en Convergence ('Convergence: Where Mathematics, History, and Teaching Interact'), revista digital de la Mathematical Association of America.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.

Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.













 ANTERIOR
ANTERIOR







































 SIGUIENTE
SIGUIENTE
