Ángulo de Maraldi
El ángulo de Maraldi es el ángulo obtuso de las caras rómbicas del dodecaedro rómbico.
Giacomo Filippo Maraldi (1665-1729) fue un astrónomo y matemático franco-italiano. Calculó el ángulo que lleva su nombre en 1712.
D'Arcy Thompson escribió:
"Kepler dedujo, a partir de la simetría de las celdas de las abejas que rellenan el espacio, que los ángulos de la base
de la celda deben ser los del dodecaedro rómbico. Swammerdam también reconoció la misma figura geométrica en las bases de las
celdas. Pero los descubrimientos de Kepler pasaron desapercibidos y Maraldi, el astrónomo y sobrino de Cassini, tiene el crédito
de haber averiguado por primera vez la forma de los rombos y de los ángulos que lo forman". [D'Arcy Thompson, Sobre el crecimiento y la forma]
Se supone que Maraldi tomó medidas reales de las celdas de las abejas. Parece que usaba colmenas de vidrio transparente para sus estudios sobre
las abejas inventadas por él. Sin embargo, actualmente se supone que en aquellos tiempos no había medios para medir estos ángulos con la suficiente
precisión. Podemos suponer que Maraldi usó algún tipo de razonamiento geométrico.
Vamos a estudiar los ángulos de las caras del dodecaedro rómbico usando Trigonometría básica.
Quizás la manera más sencilla de comprender el dodecaedro rómbico es verlo como un cubo al que se le han añadido seis pirámides de una
altura determianda.

Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.

Podríamos poner esas seis pirámides en el interior del cubo.

Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.
Una importante conclusión que podemos sacar, simplemente observando esta construcción es que los ángulos entre dos caras consecutivas
del dodecaedro rómbico es 120º. Sabes por qué? Es muy recomendable y bonito hacer esta construcción.
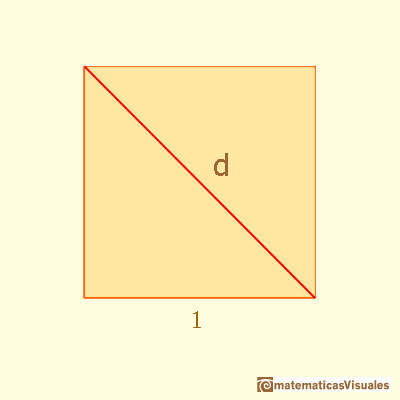
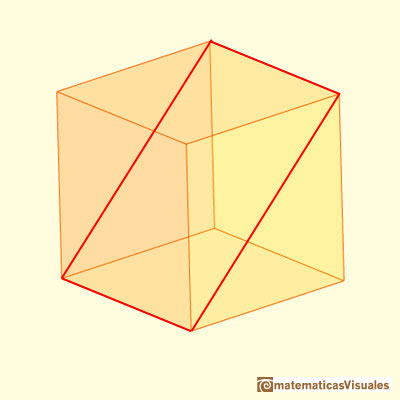
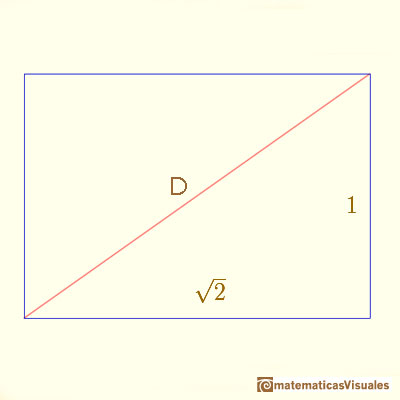
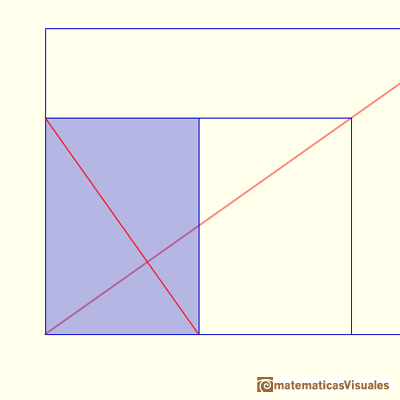
Podemos empezar estudiando el rectángulo que es una sección del cubo, que lo parte por la mitad a través de dos diagonales de caras opuestas.
Empezamos por el cuadrado. Recordamos que la diagonal de un cuadrado es:
Este rectángulo es una sección del cubo. A veces se le llama 'Rectángulo de plata'.
Es curioso que este rectángulo está relacionado con el tamaño estandarizado de papel que usamos en Europa y otras partes del mundo.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
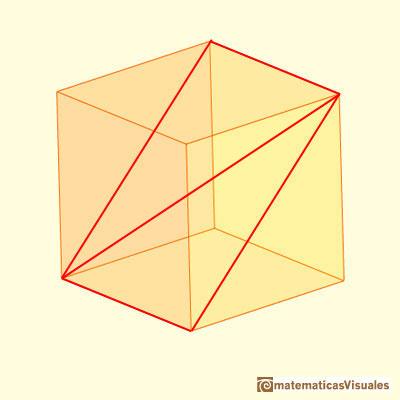
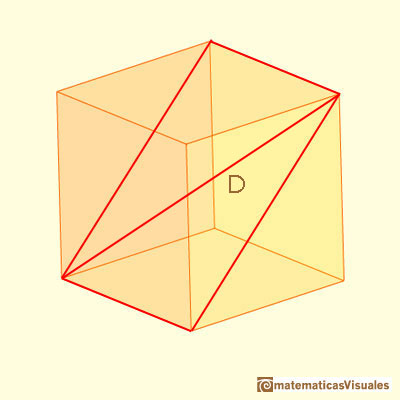
Una diagonal de este rectángulo:
Podemos calcular D como una aplicación básica del teorema de Pitágoras:
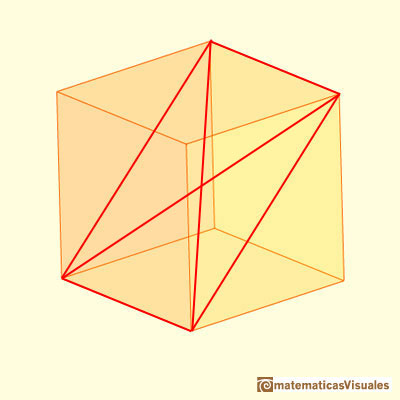
Si consideramos dos diagonales de esta sección, el punto de intersección es el centro del cubo:
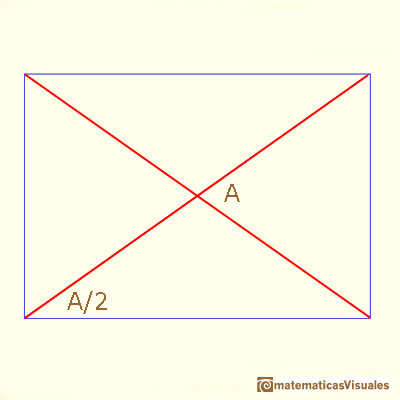
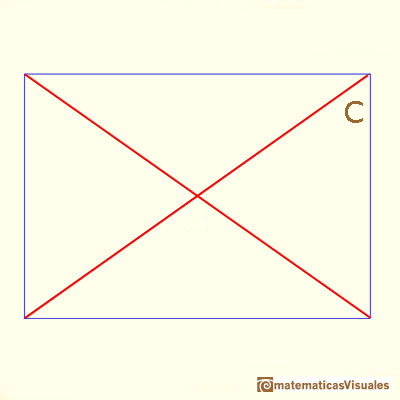
Ahora vamos a estudiar los ángulos entre dos diagonales. Para ello necesitaremos un poco de Trigonometría:
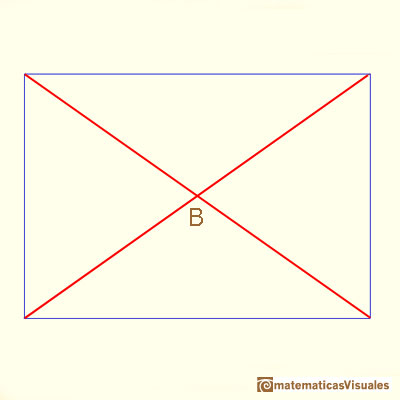
Al ángulo de Maraldi es el ángulo obtuso B (el suplementario de A):
No es difícil calcular el ángulo C:
También:
Nos encontraremos otra vez estos dos ángulos cuando estudiemos el cubo achaflanado pues nuestro rectángulo tambíen está relacionado con este
poliedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.
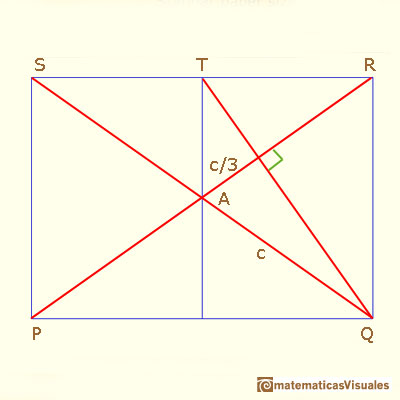
Esta es otra manera de encontrar el ángulo A:
¿Podría justificarlo?
En primer lugar, las líneas PR y QT son perpendiculares pues si rotamos 90º el rectángulo en sentido contario a las agujas del reloj...
En segundo lugar, las líneas PR y QT son dos medianas del triángulo QRS, entonces el centroide divide ...
Entonces podemos escribir cos A...
Después de Maraldi, varios matemáticos y científicos estudiaron estos ángulos. Existe un interés en comprobar si esta manera de
cerrar las celdas de las abejas es, de alguna manera, óptima y si las abejas actúan seguiendo algún instinto matemático.
El entomólogo francés Réaumur está interesado en esta cuestión y le plantea el problema a Samuel Koening, un joven matemático suizo.
Dada una celda hexagonal cerrada por tres rombos iguales, ¿cuál es la configuración que requiere la menor cantidad de material para su
construcción?
En 1739, Koening escribió una carta a Réaumur con su respuesta que era similar (pero no exactamente igual) a la que había dado Maraldi.
Parece que esta carta no fue publicada y se ha perdido. No sabemos cómo Koening estudió el problema. Pero el caso es que había una
pequeña discrepancia sobre la medida de esos ángulos.
Unos años después, en 1743, el matemático escocés
Colin Maclaurin (1698-1746) escribió
'On the Bases of the Cells wherein the Bees deposite their Honey' (que podemos traducir en 'Sobre las bases de las celdas donde
las abejas depositan su miel'). Maclaurin zanja la cuestión y lo hace usando métodos puramente geométricos (y no las técnicas
del cálculo diferencial que él ya conocía). Esto no era raro en la época.
D'Arcy Thompson escribió:
"Cuando Colin Maclaurin estudió las colmenas en Edimburgo, unos años después
de que lo hiciera Maraldi en París, resolvió el problema sin usar 'alta Geometría que no fuera conocida por los Antiguos' y
comenzó diciendo: 'Estas bases están formadas por tres rombos iguales, sus ángulos obtusos resultan ser el doble de un
ángulo que los matemáticos encuentran en cuestiones relacionadas con Máximos y Mínimos'.
El ángulo resulta ser de 109º 28' 16'', con su suplemantario de 70º 31' 44''. Este ángulo de la celdas de las abejas que
fue determinado de diferentes maneras por Maraldi, Koening y Maclaurin es el ángulo que tiene por coseno -1/3, es el
doble del ángulo que tiene por tangente raíz cuadrada de 2, y es, por un lado, un ángulo en el dodecaedro rómbico y, por otro,
es el ángulo de la simetría tetraédrica que las películas de jabón adoptan espontáneamente en una estructura tetraédrica. Ya nos
hemos referido a cuán frecuentemente aparecen y a su gran importancia".
[D'Arcy Thompson, p. 530]

Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?
Entonces, las medidas correctas eran las de Maraldi. ¿Cuál fue el error de Koening? Parece que el error procede de un error en las tablas que
Koening estaba usando. Se cuenta como anécdota que este error pudo corregirse gracias al estudio de este asunto, aparentemente poco
importante, como es el de la forma de las celdas de las abejas. Sin embargo, esas tablas eran las mismas que usaban los marinos para
calcular su posición y la
corrección del error bien pudo salvar muchas vidas en el mar.
Este ángulo es también llamado 'ángulo tetraédrico' pues es el ángulo entre dos segmentos desde el centroide de una tetraedro regular a
dos de sus vértices. También tiene su interés en Química.
El ángulo entre dos caras consecutivas de un octaedro regular también es el ángulo de Maraldi.
REFERENCIAS
Johannes Kepler - 'Strena seu De Nive Sexangula' ('Regalo de Año nuevo. Sobre el copo de nieve hexagonal', Traducción y notas de
Ana García Azcárate y Ángel Requena Fraile. Editorial Aviraneta, 2011. Este libro se puede descargar gratuitamente gracias a la generosidad
de sus autores a través del excelente sitio web de Ángel Requena 'Turismo Matemático' en su sección
Turismo Matemático. Libros descargables.
Johannes Kepler - 'De Nive Sexangula' (Tenemos una versión bilingüe en latin e inglés en
'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010.
Con notas y comentarios muy interesantes de Owen Gingerich y Guillermo Bleichmar. Las ilustraciones las realizó la matemática española Capi Corrales Rodrigáñez.
D'Arcy Thompson - On Growth And Form - Cambridge University Press, 1942. Traducción española de Ana María Rubio Díez y
Mario X. Ruiz-González publicada por Cambridge University Press.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. Una traducción española fue hecha por Luis Bou García y fue publicada por la Editorial
Salvat con el título 'Instantáneas Matemáticas' en 1986.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
W. Hope-Jones, 'The Rhombic Dodecahedron for the Young', The Mathematical Gazette, 1936.
Colin Maclaurin, 'On the Bases of the Cells wherein the Bees deposite their Honey', 1743.
D'Arcy Thompson, 'On Growth And Form' - Cambridge University Press, 1942.
L. Fejes Tóth, 'What the bees know and what they do not know', Bull. Amer. Math. Soc. 70 (1964). In
Project Euclid
D. Wallo, V. Duris, L. Rumanova, 'Geometry of bee cells rediscovered', The Electronic Journal of Mathematics and Technology.
Hermann Weil, 'Symmetry', pp. 83-92, Princeton University Press, 1952.
 SIGUIENTE
SIGUIENTE

Queremos cerrar un prisma hexagonal como lo hacen las abejas, usando tres rombos iguales. ¿Qué forma deben tener estos tres rombos para cerrar el prisma con la menor superficie?
 ANTERIOR
ANTERIOR

La Humanidad ha estdo siempre fascinada por cómo las abejas construyen sus panales. Kepler relacionó la forma de los panales con un poliedro que llamamos dodecaedro rómbico.
MÁS ENLACES

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Añadiendo seis pirámides a un cubo podemos construir nuevos poliedros que tienen veinticuatro caras triángulares. Para unas determinadas pirámides obtenemos un dodecaedro rómbico que tiene doce caras rómbicas.

Podemos construir un dodecaedro rómbico añadiendo seis pirámides a un cubo. Este hecho tiene interesantes consecuencias.

Podemos llenar el espacio con dodecaedros rómbicos sin dejar huecos.

Una cadena de seis pirámides puede plegarse hacia dentro y formar un cubo y puede plegarse hacia fuera y colocarse sobre otro cubo y formar un dodecaedro rómbico.

Kepler relaciona el dodecaedro rómbico con el apilamiento de balas de cañón. Si se comprime un determinado apilamiento, las balas se deforman en este poliedro.

Estudiando el empaquetamiento de esferas obtenemos el dodecaedro rómbico y el dodecaedro trapezo-rómbico. Su dual es el cuboctaedro girado.

A partir de un conocimiento básico del dodecaedro rómbico se puede calcular rápidamente la densidad del empaquetamiento óptimo de esferas.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Tetraxis es un puzle muy interesante, sencillo y bonito, diseñado por Jane y John Kostick. Estudiaremos algunas propiedades de este juego y su relación con el dodecaedro rómbico. Plantillas para construir un Tetraxis con cartulina e imanes. El rompecabezas hecho con impresión 3D.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.

Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.












 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR



































