El Teorema del Hexagrama de Pascal
Blaise Pascal (1623-1662) fue un matemático y filósofo francés.
El teorema que vamos a estudiar se conoce como teorema de Pascal o del Hexagrama místico. Fue enunciado por Pascal a la edad de 16 años.
La naturaleza de este teorema es proyectiva. En el plano proyectivo dos rectas siempre se cortan. En la geometría euclídea (y también en la geometría afín) dos rectas pueden ser paralelas y no cortarse. Veremos que en el enunciado del teorema de Pascal lo fundamental son las relaciones de incidencia: puntos que están en rectas, rectas que pasan por puntos e incidencia de rectas.
El teorema de Pascal, en su forma general proyectiva, se refiere a una cónica. En esta página vamos a explorar el teorema en un caso particular: cuando la cónica es una circunferencia. Es decir, vamos a estudiar este teorema proyectivo en el plano euclídeo que, en principio, nos puede resultar más familiar.
Esto tiene la ventaja de que la circunferencia es sencilla pero también tiene desventajas. Veremos más adelante que hay que considerar los casos especiales de rectas paralelas.
Vamos con el enunciado del teorema:
Teorema de Pascal: Si se inscribe en una circunferencia un hexágono, los puntos de intersección de lados opuestos son colineales.
La recta que determinan esos puntos se llama recta de Pascal.
La demostración de este teorema se puede encontrar en cualquier libro de geometría proyectiva.
Para ver la animación y manipular la aplicación interactiva se necesita Adobe Flash Player.
Se pueden mover los puntos y ver las diferentes configuraciones.
Los lados opuestos están dibujados del mismo color. En general, prologamos los lados para que se corten y los puntos de intersección forman la recta de Pascal.
En su forma proyectiva, el teorema de Pascal se refiere a un hexágono inscrito en una cónica. Desde el punto de vista de la geometría euclídea ya sabemos que elipses, parábolas e hipérbolas son cónicas o secciones cónicas. El teorema de Pascal se cumple en todos esos casos y podríamos sustituir la palabra circunferencia por cónica en todo lo que sigue. La circunferencia es un caso particular de elipse y es la más sencilla de las secciones cónicas.
Empezamos con una circunferencia y un hexágono inscrito en ella.
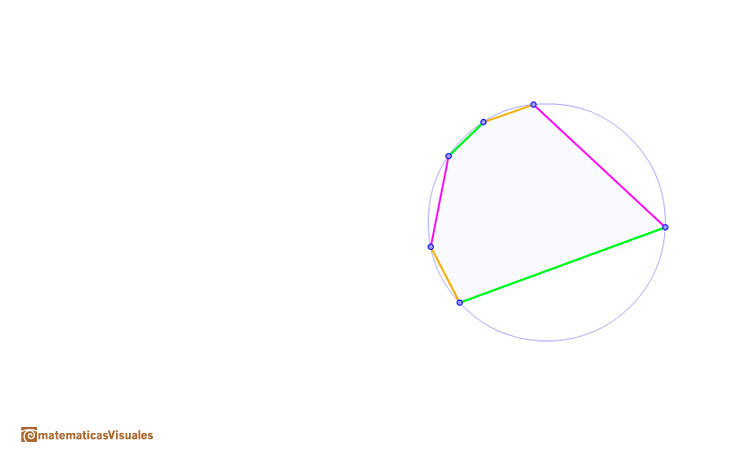
Los pares de lados opuestos se cortan en tres puntos que están alineados.
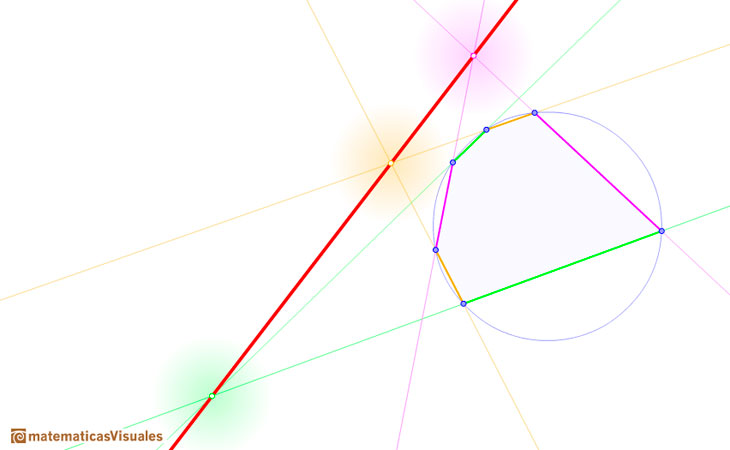
Podemos mover los puntos y ver que no es necesario que el hexágono sea convexo. Por ejemplo:
Si dos vértices del hexágono coinciden entonces consideramos que el lado que forman es la recta tangente. El hexágono es ahora un pentágono y el teorema también se verifica.

Si dos pares de puntos coinciden entonces tenemos un cuadrilátero. Entonces un par de lados opuestos y las tangentes a dos vértices opuestos se cortan en una línea recta.

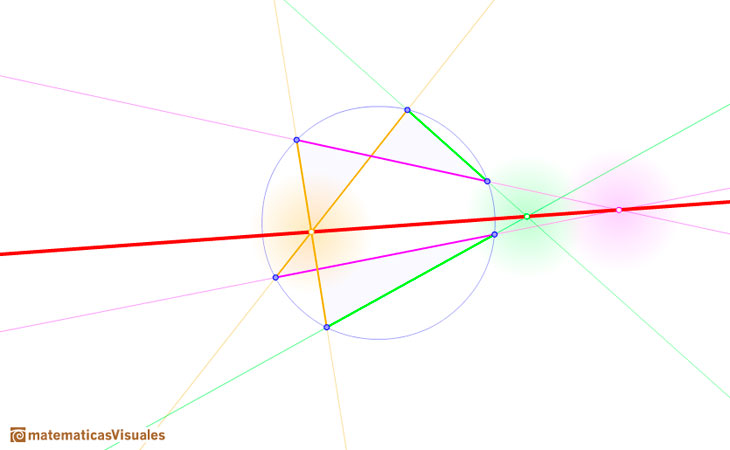
En el caso de un triángulo inscrito en una circunferencia se cumple que cada lado y la tangente en el vértice opuesto se cortan en tres puntos que están alineados.
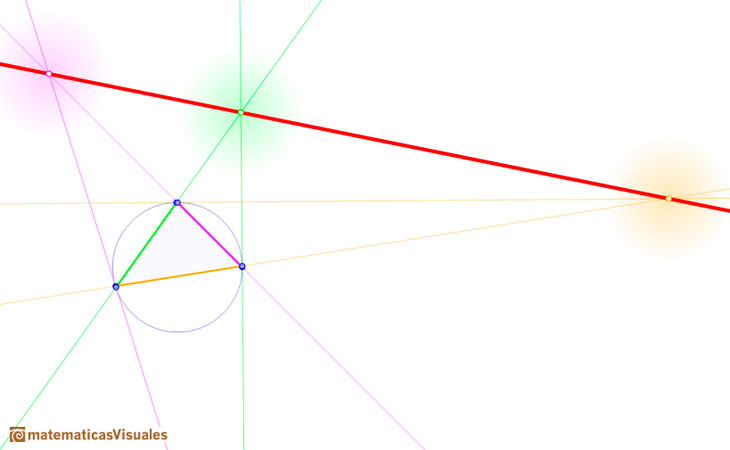
En el plano proyectivo dos rectas diferentes siempre se cortan en un punto. Sin embargo, cuando consideramos el teorema de Pascal en el plano euclídeo el teorema sigue siendo cierto pero tenemos que hacer algunos ajustes para considerar los casos especiales cuando los lados opuestos son paralelos.
Si solo dos lados opuestos son paralelos entonces la línea de Pascal determinada por los puntos de intersección de los otros dos pares de lados opuestos es paralela a los lados paralelos.
Hay una manera muy intuitiva de obtener un modelo del plano proyectivo a partir del plano euclídeo (o también partiendo del plano afín) es añadir al plano una recta 'en el infinito'. Cada familia de rectas paralelas determina un punto 'en el infinito' y todos esos puntos forman la recta 'en el infinito' que añadimos al plano.
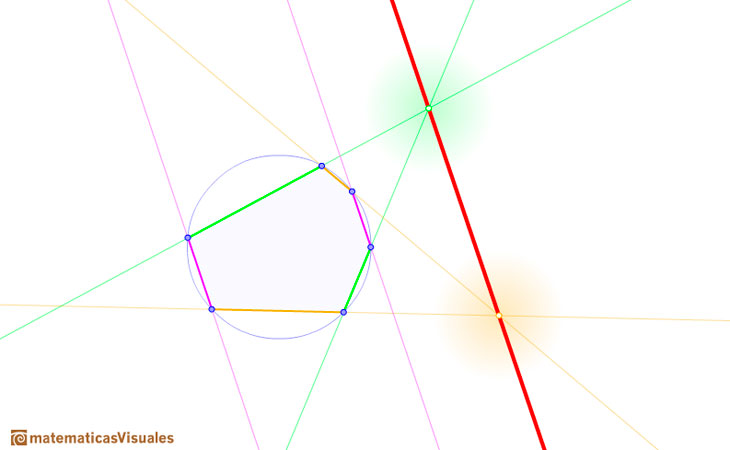
En el ejemplo anterior, cuando dos lados opuestos son paralelos, podemos decir que la recta de Pascal pasa por los tres puntos de intersección de los pares de lados opuestos: dos de esos puntos son 'ordinarios' y el tercero es el punto 'en el infinito' que determinan los dos lados paralelos. Desde el punto de vista del plano proyectivo, todos los puntos tienen la misma naturaleza.
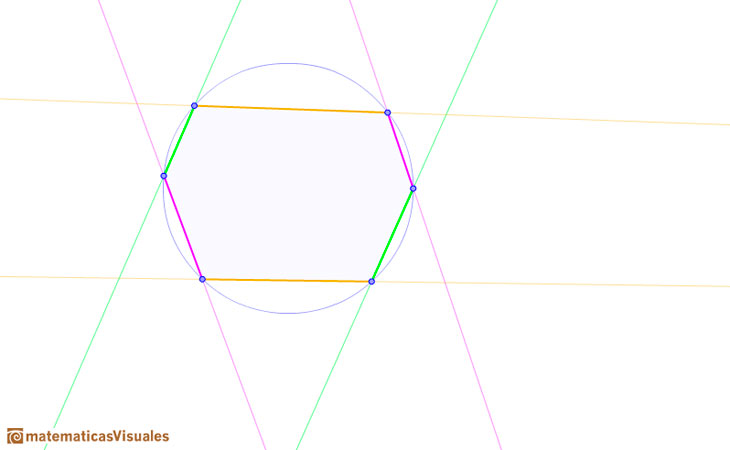
Si dos pares de lados opuestos son paralelos entonces los tres pares de lados opuestos son paralelos. En este caso la recta de Pascal sería la recta 'en el infinito'.
El teorema de Pascal es muy bonito y uno de los objetivos de mostrarlo aquí es estimular el deseo de estudiar geometría proyectiva que es una rama de la Geometría muy relacionada con el Arte y la perspectiva.
Dos rectas se pueden considerar una cónica degenerada. Entonces el teorema también es cierto. Esta propiedad era conocida en la Antigüedad y se conoce como teorema de Pappus.
En el plano proyectivo cada teorema tiene su teorema dual. El dual del teorema de Pascal se conoce como teorema de Brianchon.
REFERENCIAS
H.S.M. Coxeter - 'Projective Geometry' - Blaisdell Publishing Company, 1964.
H.S.M. Coxeter - 'The real projective plane', Springer-Verlag, Third edition, 1993.
Howard Eves - 'A Survey of Geometry', Allyn and Bacon, Inc., 1972.
 SIGUIENTE
SIGUIENTE
MÁS ENLACES
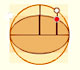
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.
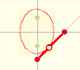
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.
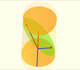
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
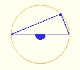
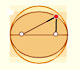
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.
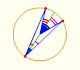
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.