Ya hemos estudiado el comportamiento asintótico de varias funciones racionales. Es decir, cómo es
o cuál es la tendencia de una función cuando el valor de la variable x es muy grande en valor absoluto.
El caso más sencillo es cuando el grado del numerador es menor que el grado del denominador. Estas funciones racionales se llaman propias.
Las funciones racionales propias tienen una asíntota horizontal y=0, es decir, el eje de abcisas. Cuando consideramos valores de x grandes
(tanto positivos como negativos) el valor de una función racional propia es muy pequeño y lo podemos hacer tan pequeño como queramos tomando
valores de x suficientemente grandes. El ejemplo básico es la hipérbola equilátera (proporcionalidad inversa).
Si el grado del numerador es igual al grado del denominador, la función racional tiene una asíntota horizontal y=k.
Ya hemos visto ejemplos cuando el grado del numerador y denominador es 1 o cuando el grado del numerador y
denominador es 2.
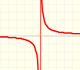
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
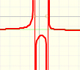
Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).
Si el grado del numerador es exáctamente uno más que el grado del numerador la función racional tiene una asíntota oblicua.
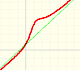
Para valores grandes en valor absoluto de la variable x algunas funciones se comportan como una recta oblicua. A esta recta la llamamos asíntota oblicua de la función.
En general, si dividimos el numerador de una función racional por su denominador obtenemos un polinomio en el cociente Q(x)
y un polinomio que es el resto. El grado del resto es menor que el grado del denominador. Este resto, cuando lo dividimos entre el denominador, va a
contribuir muy poco cuando calculemos los valores de la función con valores de |x| grandes.
Una función racional se puede descomponer como la suma de un polinomio (el cociente) más una función racional propia.
El comportamiento asintótico de la función racional sigue el comportamiento del polinomio del cociente: f(x) se comporta como Q(x) para valores grandes de x.
Vamos a empezar con el caso de una función racional que tiene un polinomio de grado 2 como polinomio cociente, un número como resto y un polinomio de grado 1 en el
denominador.
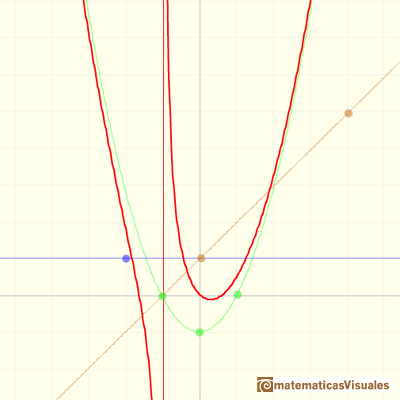
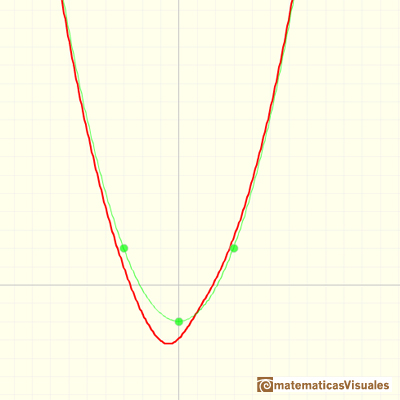
En el primer applet podemos jugar con los tres elementos de este tipo de funciones racionales:
el polinomio del cociente (en verde, una parábola), el numerador (en este caso, un número, en azul una recta horizontal) y
el denominador (una recta, en naranja).
Por ejemplo:
La fórmula para la gráfica anterior es:
La ecuación del polinomio del cociente (función asintótica) es:
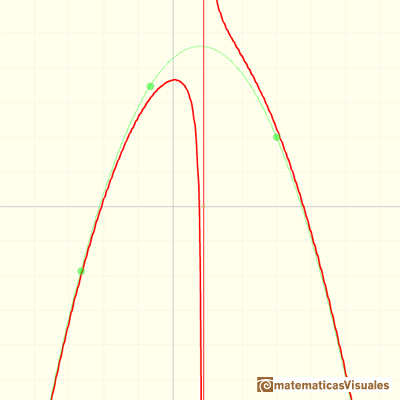
Otro ejemplo:
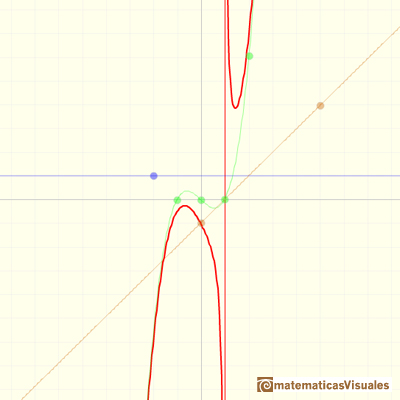
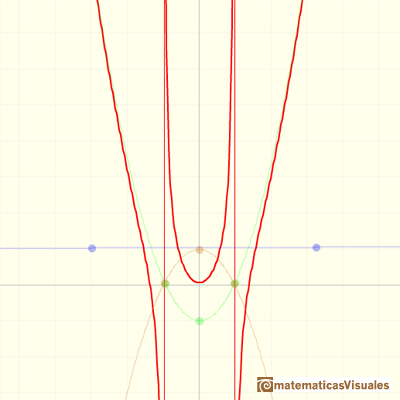
En el siguiente applet podemos ver funciones racionales que tienen un polinomio de grado 3 como cociente, un número como resto y un polinomio de grado 1 en el denominador.
Los tres elementos de este tipo de funciones racionales son:
Un polinomio cociente (en verde, una función cúbica), un numerador (un número, en azul, una recta horizontal) y el denominador (una recta naranja)
Por ejemplo:
La formula de la gráfica anterior es:
La ecuación del polinomio del cociente (función asintótica) es:
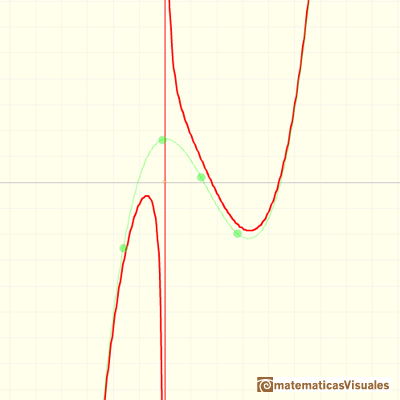
Otro ejemplo:
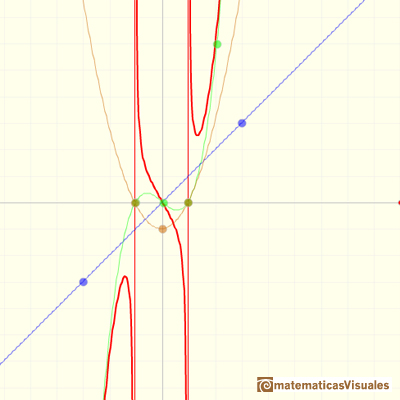
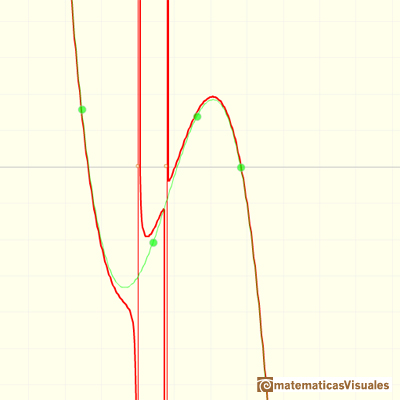
En el último vídeo de la serie podemos ver funciones racionales que tiene un polinomio de grado 3 como polinomio cociente,
un polinomio de grado 1 como resto y un polinomio de grado 2 en el denominador.
REFERENCIAS
G.E. Shilov, Calculus of Rational Functions, Mir Publishers, Moscow.
I.M. Gelfand, E.G. Glagoleva, E.E. Shnol, Functions and Graphs, Dover Publications, Inc., Mineola, New York.
MÁS ENLACES

Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.

Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
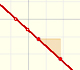
Dos puntos determinan una línea recta. Como función son las funciones afines. Estudiaremos la pendiente de la recta y como podemos obtener la ecuación de la recta que pasa por dos puntos. Estudiaremos el corte con el eje de abcisas.
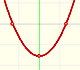
Las funciones cuadráticas son polinomios de grado 2. Sus gráficas son parábolas. Para encontrar los puntos de corte con el eje de abcisas tenemos que resolver una ecuación. El vértice de la parábola es un máximo o mínimo de la función.
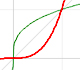
Potencias con exponente natural son funciones importantes pues son la base de los polinomios. Sus funciones inversas son las raíces que son funciones potencia con exponente racional positivo.
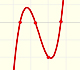
Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.

Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
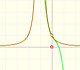
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
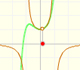
La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.
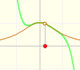
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.

Las potencias de exponente natural tienen un cero de multiplicidad n.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.

Un polinomio de grado n tiene n ceros o raíces.
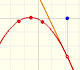
La derivada de una función cuadrática es una función afín, es decir, es una línea recta.
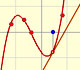
La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.




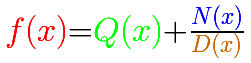
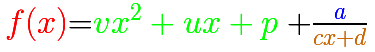
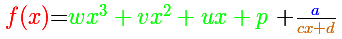
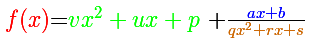
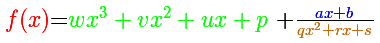
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR







































